タイヤバランサーの論文
ぜんぜん違うもの調べてたら。。出てきたので思い付きでまた調べてしまったシリーズ(笑)
オープンアクセスの論文を少しみてたら。。こんな論文が。。
Design and Development of Wheel Balancing Machine Experimental Setup
この論文では、ArduinoでDynamic balanceをGセンサで取って推定するってことやってて。。どこにおもりをつけるといいのか??までは解いていなかった(笑)
で。。そういや。。タイヤバランサーの仕組みってどうなってたんだっけ??って。。 Solidなものだと、たぶん解析的に解けるはずで。。軸につけて回転させて、軸の振動(力)のX・Y・Z軸から求まるんじゃないかな?? って思ったけど。。
どうやるんだっけ??(笑)
本とか、論文っていまだにいろいろ出ている分野なんですね。。とか思ったり。。
https://www.instructables.com/Dynamic-Motor-Balancing-with-Sugru-and-an-iPhone/
https://scholarsmine.mst.edu/cgi/viewcontent.cgi?article=5896&context=masters_theses
BASICのプログラムで作られてた~ なんか懐かしいです。
古くに解かれている問題だから。。Gnu Octave や Matlabでサンプル落ちてるんじゃないのかな?って見てみると
https://www.intechopen.com/chapters/46862
https://www.researchgate.net/publication/343083277_Investigating_aids_for_teaching_the_balancing_of_rotating_masses
https://web.archive.org/web/20210716193823id_/https://dergipark.org.tr/en/download/article-file/1486475
ありましたが。。プログラム自体はなかった(笑)
Wikiだと、この
https://en.wikipedia.org/wiki/Balancing_of_rotating_masses
Python でタイヤ振動かくと。。
# おもりの重さの異なる複数のケースに対する遠心力を計算する関数
def calculate_centrifugal_force(mass_weight):
# 重心の計算
x_center_mass = (mass_weight * (radius_wheel - thickness_wheel)) / total_mass
# 遠心力の計算(三次元成分)
centrifugal_force_x = total_mass * (angular_velocity ** 2) * x_center_mass * np.cos(angular_velocity * t)
centrifugal_force_y = total_mass * (angular_velocity ** 2) * x_center_mass * np.sin(angular_velocity * t)
centrifugal_force_z = total_mass * (angular_velocity ** 2) * x_center_mass * np.sin(phi)
return np.sqrt(centrifugal_force_x**2 + centrifugal_force_y**2 + centrifugal_force_z**2)
# z方向の角度(仮定)
phi = np.pi / 4 # 45度
# 重さの異なるおもりに対する遠心力を計算
weights = [2 / 1000, 3 / 1000, 4 / 1000, 5 / 1000] # kg
forces = [calculate_centrifugal_force(weight) for weight in weights]
# グラフのプロット
for force, weight in zip(forces, weights):
plt.plot(t, force, label=f'{weight * 1000}g')
plt.xlabel('Time (s)')
plt.ylabel('Centrifugal Force (N)')
plt.title('Centrifugal Force over Time for Different Weights')
plt.legend()
plt.grid(True)
plt.show()
# おもりの重さを変化させた場合の各RPMでの遠心力を計算し、プロットする関数
def plot_force_rpm_different_weights(rpms, weights):
plt.figure(figsize=(10, 6))
for weight in weights:
forces_rpm = [calculate_force_rpm(rpm, weight / 1000) for rpm in rpms] # 重さをkgに変換
plt.plot(rpms, forces_rpm, label=f'{weight}g')
plt.xlabel('Rotation Speed (RPM)')
plt.ylabel('Centrifugal Force (N)')
plt.title('Centrifugal Force vs. Rotation Speed for Different Weights')
plt.legend()
plt.grid(True)
plt.show()
# おもりの重さのリスト(2g, 3g, 4g, 5g)
weights = [2, 3, 4, 5]
# RPMの範囲を設定
rpms = np.linspace(1, 1000, 100) # 1 RPM から 1000 RPM
# おもりの重さを変えてグラフをプロット
plot_force_rpm_different_weights(rpms, weights)
こんな感じか??

回転が上がると、偏りの重さが思いほど力がかかるので、重さを特定するのはこれの逆するのかな?
# 2gのおもりをホイールの軸から0°、10°、20°の位置にずらした場合のX軸・Y軸の遠心力を計算する関数
def plot_force_xy_time_different_angles(t, weight, angles):
plt.figure(figsize=(12, 6))
# おもりの重さ(kg)
mass_weight = weight / 1000
for angle in angles:
# 角度をラジアンに変換
angle_rad = np.radians(angle)
# 重心の計算
x_center_mass = mass_weight * (radius_wheel - thickness_wheel) * np.cos(angle_rad) / total_mass
y_center_mass = mass_weight * (radius_wheel - thickness_wheel) * np.sin(angle_rad) / total_mass
# X方向とY方向の遠心力の計算
centrifugal_force_x = total_mass * (angular_velocity ** 2) * x_center_mass * np.cos(angular_velocity * t)
centrifugal_force_y = total_mass * (angular_velocity ** 2) * y_center_mass * np.sin(angular_velocity * t)
# グラフにプロット
plt.plot(t, centrifugal_force_x, label=f'X-axis {angle}°')
plt.plot(t, centrifugal_force_y, '--', label=f'Y-axis {angle}°')
plt.xlabel('Time (s)')
plt.ylabel('Centrifugal Force (N)')
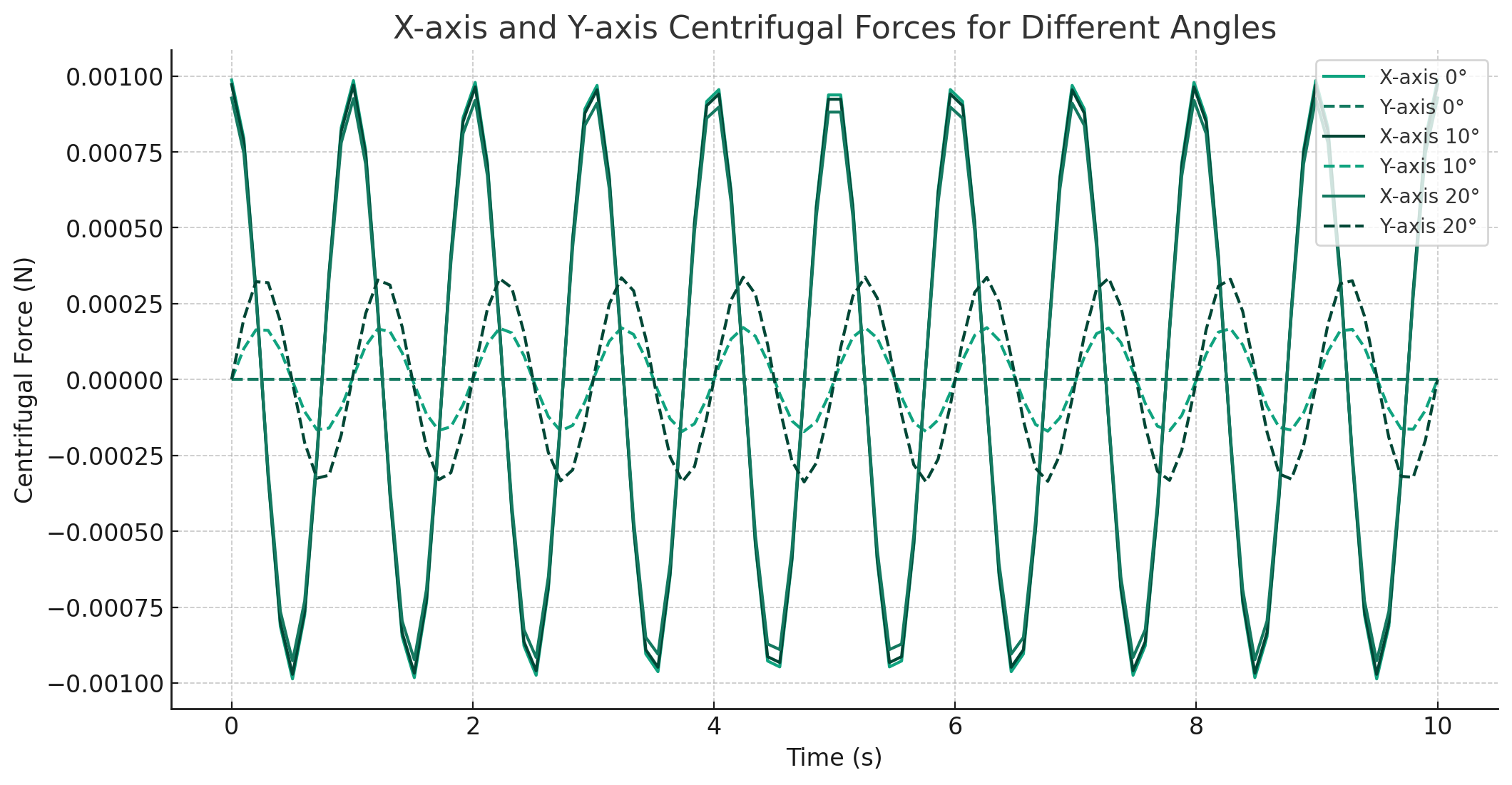
plt.title('X-axis and Y-axis Centrifugal Forces for Different Angles')
plt.legend()
plt.grid(True)
plt.show()
# おもりの角度のリスト(0°, 10°, 20°)
angles = [0, 10, 20]
# X軸・Y軸の力を時間に対してプロット(2gのおもり)
plot_force_xy_time_different_angles(t, 2, angles)

この位相で場所を特定するのかな??
って。。これを調べてたんじゃない(笑)
コメントを残していただけるとありがたいです