目次
あれ?どんな図になるんだっけ??
機械・制御系なので、伝達関数は授業聞いてたけど、インピーダンス・アドミッタンスは、聞いてなかった(笑)この歳になって、等価回路を計算したりをしてみて。。ひょっとしてよくわかってない??って。。思い出したので。。ちょっと一回、まとめておこうかな?と。。
https://tom2rd.sakura.ne.jp/wp/?s=Spice
こんなPythonライブラリーやSPICEの紹介しているのにね(笑)
時間関数と伝達関数(ラプラス変換)
時間領域と複素数領域で式を変換することをラプラス変換っていいます。制御ではよく使います。時間 tで変化する関数を複素数領域に変換して計算簡単にやろうってことですね。
$$f(t)\Leftrightarrow F\left( s\right)$$
ラプラス変換自体式は、
$$\mathcal{L}{f(t)} = \int_0^\infty f(t) e^{-st} \mathrm{d}s $$
この式を理解しようとすると。。めんどくさいけど。。
$$e^{-st}$$
をかけてsで積分している。
ラプラス変換や、Wikiラプラス変換 を参照してみるといい。
でも制御しないのなら理解する必要ないかも??(笑) 時間の関数を複素数で変換したってことだけでいいかも?
ちなみに。。SymPyでやると。。なぜかIntegralとか動かないから。。素直にControlとか使った方がわかりやすいですね。
こちらでは、SymPyでのやり方も載ってますが。。むっちゃ時間かかるので、やめた方が良さそうです。Octaveの方がいいかも。。
過渡応答をみたいようなときに、入力波形のラプラス変換した式 と 伝達関数をかけて、逆ラプラス変換すると、時間波形が出てくる。。っていう感じで簡単に式が表せるってことだけ知ってたらいいような気がするんだけど。。
VやIを求める時
AからBに伝わるのに変換される伝達関数がF(s)の時
入力の時間関数u(t)をラプラス変換した関数がU(s)とすると、出力波形は、O(t)は
$$o(t)=\mathcal{L}^{-1} \left\{F(s)\times U(s)\right\}$$
ってなるってことだけ知ってれば。。 伝達関数が、インピーダンス Z であらわされている時は、V=Z*I で 電流入れると電圧が求まる。 アドミッタンス Yの時は、I=Y*Vで書けるってことを知ってれば使えると思う。。
あとは変換表で探す。。あるいはもうMatlabとかOctaveつかっちゃえ!
一応、Python+SympyでLaplace変換を行うJupyterNotebookをここに置いておきます。
変換表を作ったり、関数の形が見えるようにしてあります。
ただしSympyはIntegralやlaplace.transformsの関数で、計算できない時がありますので、注意です。
$$ \frac{1}{a + s} $$
という伝達関数に、
下のようなステップ関数を入れると

減衰 時間波形がでてくる。。とかやってます。
一応、伝達関数の形(グラフ)もかけるように作りました。
フィルタや素子などの周波数特性を求める時
周波数特性などを求める時は、伝達関数は、Vin(入力) Vout(出力)の比で求めます
$$ \frac{Vout}{Vin} $$
の関係で出てくる伝達関数がフィルタなどの特性(周波数特性)と呼ばれるものですね。

これの伝達関数ででも求められるし、複素数でも求められる
s=jω
なので、プログラムなどでは、ラプラス変換要らないでnumpyで計算できる
インピーダンス・アドミッタンスと伝達関数
複素数表記
| インピーダンス | アドミタンス | |
| 抵抗 | R | 1/R (= G ) |
| インダクタ | jωL | 1/(jωL) |
| コンデンサ | 1/(jωC) | jωC |
伝達関数表記
| インピーダンス | アドミタンス | |
| 抵抗 | R | 1/R (= G ) |
| インダクタ | sL | 1/(sL) |
| コンデンサ | 1/(sC) | sC |
上のフィルタは、このように、Voutのインピーダンスが十分高いと、電流は、Voutに流れないので、電流Iは、R1にもC1にも同じ電流が流れるので、分圧で表されて

Vinから見たインピーダンスは、R+1/jωC ラプラス変換だと R+1/sC
Voutから見たインピーダンスは、1/jωC 又は 1/sC だから
Vin = Zin × I
Vout= Zout × I
で Vout/Vin は 伝達関数で表すと
$$ \frac{Vout}{Vin}= \frac{\frac{1}{sC}}{R+\frac{1}{sC}}=\frac{1}{1+sCR} $$
ってなる。(分母分子にsCかけて少し簡単にしてる)
Sympyで伝達関数で、ボード線図を書いてみる
Sympyだと、TransferFunctionを定義して、physics.controlというライブラリがあって、そのままボード線図とかかけます。

ωを角速度(rad/sec)になっていますが。。
bode_plot(tf3,freq_unit='Hz',phase_unit='deg')
とすると、周波数と角度でも出せます
 $$ \omega \equiv \frac{d\theta}{dt}=\frac{2\pi}{T}=2\pi f $$
$$ \omega \equiv \frac{d\theta}{dt}=\frac{2\pi}{T}=2\pi f $$
になってるかな??(笑)なってなさそうな気がする。。 ω=f/2π で式を入れないといけなさそうですね。
ボード線図 は、 ゲイン(|Gain|) と フェーズ を周波数(rad/sかdeg)
インパルス応答や、ステップ応答 の過渡応答も見れます。

伝達関数としてわかっていて、そこそこ複雑なものも、Pole Zero Plotもできるので安定性判別とかも簡単にできそうですね。
SymPy以外でも、ControlというライブラリにMatlab互換の関数があるようで、これでも同様のことはできそうです。
https://python-control.readthedocs.io/en/latest/index.html
複素数で計算してみる Numpy
さっきの
$$ \frac{Vout}{Vin}= \frac{\frac{1}{sC}}{R+\frac{1}{sC}}=\frac{1}{1+sCR} $$
s=jωを代入して、
分数なので、これを a+jb の形にするために、共役複素数を上下にかけると。。その形式になるんですが。。PythonとNumpyでそのまま数値的に計算できます。
omega = numpy.logspace(-2, 10, 1000) s = omega*1j r=100 c=1e-6 G1 = (1/(s*c))/(r+1/(s*c))
と真ん中の式そのまま伝達関数として書いても、代入してくれます。
角周波数(rad/sec)でBode書くと

周波数をHzにするには、frequency = ω/2π とするとよくて

ちゃんと周波数変わってますね。自分で作ると(笑)
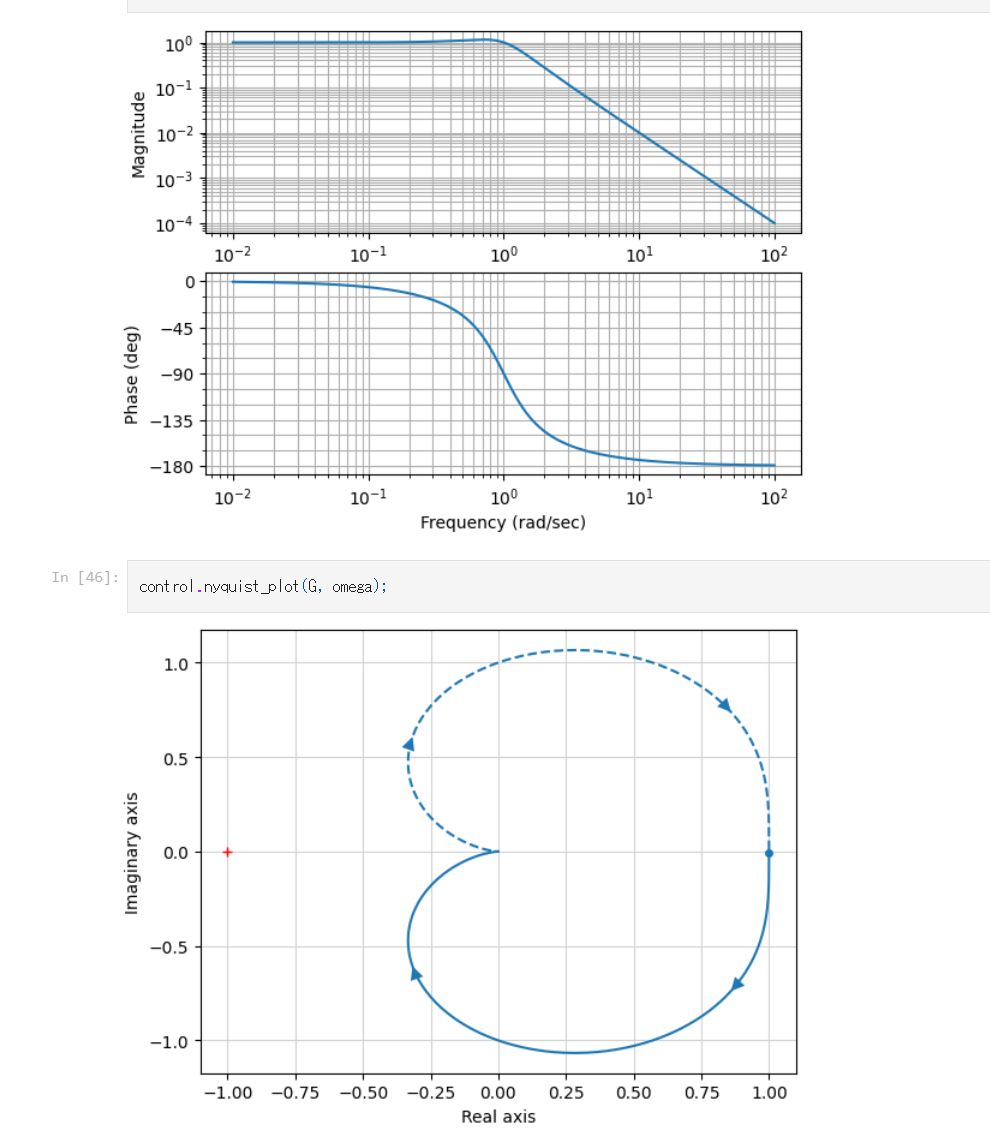
Nyquist は、real と imaginary を軸にして書いているだけなので、下記のように書けます。

Control ライブラリでの例も乗っけたNotebookは、こちらにおいてます
LRC回路のインピーダンスをBodeとNyquistで書く
が本当はいろいろやりたかったことだけど。。ここまでで長くなったので、またつづきます。
いろいろGithubにipynbをあげているので、参考に
https://github.com/tom2rd/EMC-sim/tree/master/impedance.py/Laplace-impedance
PS. 今回数式は、MathJax – LaTeXを使いました。
ここ便利です。
LaTexで数式どう描くか??忘れた時は。。
http://www.hostmath.com/
https://webdemo.myscript.com/views/math/index.html
コメントを残していただけるとありがたいです