ラプラス変換 と 方程式と 鶴亀算
電気回路をラプラス変換で、計算すると簡単って。。
今では使う人も少ないだろうけど(笑)
つるかめ算でやってた計算を、方程式でやったら一般的で簡単にできる!っていうのと同じような感じなんですよね。
つるかめ算だといろんな法則とかやり方を覚えなきゃいけないけど、方程式だと、x や yといったわからないことを変数を使って式にすれば、いろんな問題が同じ考え方で解ける。。
ラプラス変換も、交流の回路を、伝達関数に置き換えれば、簡単な式になってそれを数値に置き換えれば、周波数応答がわかるし、逆ラプラス変換で時間応答もわかる。
高周波をやると、どうしても素子の特性とかが、純粋な抵抗になってなかったり、少し複雑な回路のふるまいを把握するのに、シミュレーションが有効なんですが、そのシミュレーションを行うには、素子の特性や、回路の形、系だと、そのモデルを作ることがとっても重要なんですよねぇ・・
とかいう僕も、久しぶりにGain Phaseアナライザを使って、とったデータから定数を推定してみようって思って。。impedance.pyとかやってみて。。そうだったよなって思い出したので、少しまとめておいてるシリーズです(笑)
高周波での特性 等価回路いろいろ
たぶん大学の教科書とかにはわりと最初の方に出てくるんでしょうけど。。こういうのを使う人はあんまりいないのかな?
電池の特性とか半導体の特性とか複雑な回路の前に、とっても単純な抵抗、キャパシタ、インダクタも、高周波で使うときは、こういう等価回路において計算したりしますねぇ。。
RLCの等価回路
いろんなメーカのサイトにSPICEモデルなどがすでに出されているんですが。。ただの抵抗や、キャパシタなんか本当にいろんな等価回路が使われていて。。その定数をきちんと出していたりするんですよね。ちょっと例と、全部は用意するのがめんどくさかったので、キャパシタまでしかないけど。。JupyterNotebook類も用意したので、特性など見てみて
| 等価回路 | 合成インピーダンス
ラプラス式 |
メモ | |
| 抵抗 |  |
$$\frac{1}{C_{0} s + \frac{1}{L_{0} s + R_{0}}}$$ | Rsという抵抗成分に表皮効果だったり巻き線部分だったりのインダクタンスLsがあり、SMDなどの両端の金属部の寄生容量があるような等価回路 |
| キャパシタ |  |
$$ L_{0} s + R_{0} + \frac{1}{C_{0} s}$$ | 容量Cに、内部抵抗ESRと内部インダクタンスESLがある回路 |
| キャパシタ |  |
$$L_{0} s + R_{1} + \frac{1}{C_{0} s + \frac{1}{R_{0} + \frac{1}{C_{1} s}}}$$ | タンδとか言われる誘電損失をC2とRdlで表した回路 |
| インダクタ |  |
$$R_{0} + \frac{1}{C_{0} s + \frac{1}{L_{0} s}}$$ | インダクタンスLの巻き線に寄生する容量と、抵抗Rsで表した回路 |
| インダクタ |  |
$$\frac{1}{C_{0} s + \frac{1}{L_{0} s + R_{0}} + \frac{1}{R_{1}}}$$ | インダクタのピークのインピーダンスをきちんと出すためにRpを入れた回路 |
| インダクタ |  |
$$\frac{1}{C_{0} s + \frac{1}{R_{0} + \frac{1}{\frac{1}{R_{2}} + \frac{1}{R_{1}} + \frac{1}{L_{1} s}}}}$$ | こういうのもある。 |
| ダイオード |  |
$$R_{0} + \frac{1}{C_{0} s + \frac{1}{R_{1}}}$$ | 非動作時逆方向のダイオードの例 |
| ダイオード |  |
$$\frac{1}{C_{1} s + \frac{1}{C_{0} s + \frac{1}{R_{0}}}}$$ | 上記と同様 |
Pythonでの計算例
まぁいろいろな回路例がありますが、非線形になってないと、式でPythonで簡単に計算できます。
計算と特性例をラプラス変換そのもので計算したのと、Numpyで数値的に計算したものの例をおいておきます。
- EquivalentCircuit-Resistor-Sympy.ipynb
- EquivalentCircuit-Capacitor-Sympy.ipynb
- EquivalentCircuit-Capacitor2-Sympy.ipynb
などを見てみてください。 全部はないけど。。ラプラス式と値だけ変えればいろいろ使えるかと思います。
周波数特性の例
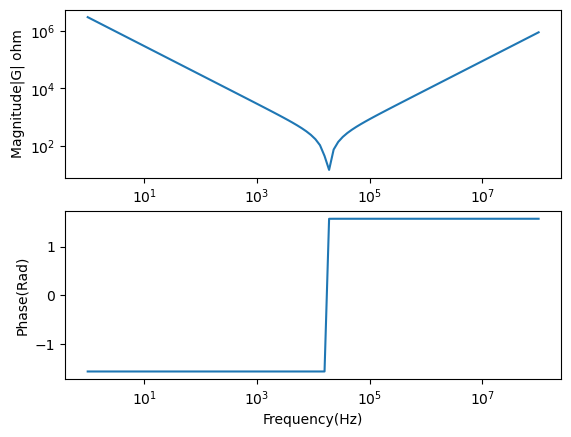
100k ohmの実際のSMD抵抗の例


コンデンサの例
ゲインフェーズで見たまんまですね。。

さてさて。。 こんな基礎的なところを書いているようじゃ。。
電気化学や結晶のところとかをうまく表現できるようになるのかな??(笑)
コメントを残していただけるとありがたいです